A Report on

Stair climbing mechanism

The Scepter

 

Submitted by

Subhasis Behera (002120169)

 

 

 

Under the guidance of

Dr. Rakesh Chandra,

HOD, Department of Mechanical Engineering.

 

 

 

 

 

 

 

Dr. B. R. Ambedkar National Institute of Technology, Jalandhar, Punjab – 144011.

 

ACKNOWLEDGEMENTS

 

We would like to express my sincere thanks to our Project Guide, Dr. Rakesh Chandra, Professor, Head, Dept. of Mechanical Engg., National Institute of Technology, Jalandhar for his guidance and encouragement throughout the project.

 

We are really thankful to Mr. Promod Kumar, Mr. M. K. Tiwari, and Mr. Raman Bedi, Professors, Mechanical Engg. Dept. for their continuous support during this work.

 

We also extend heartfelt gratitude to all those who helped us for the successful construction of the model.

 

 

 

INDEX

 

 

i

ii

Front Page ……………………………………………………………………...........

iii

Acknowledgements ………………………………………………………………….

1

Index ………………………………………………………………………………...

2

Abstract ……………………………………………………………………………..

7

1 Introduction ………………………………………………………………………

12

2 Design & Construction ……………………………………………………………

18

3 Kinematic Analysis ……………………………………………………………….

21

4 Modeling & Animation ……………………………………………………..

a

5 Conclusions …………………………………………………….. ……………….

References …………………………………………………………………………...

 

 

 

 

 

ABSTRACT

 

Walking machines are advanced alternatives to wheeled locomotion which find applications where wheeled systems cannot be operated. Of these, Stair-climbing machines have come out to be the field, to have been revolutionized in the recent past. Basic purpose of these machines remains serving the handicapped which becomes the objective of the model demonstrated in this paper.

The paper is about an Experimental model of a Stair-climbing Mechanism – The scepter, which was designed and constructed by me in Dr.B.R.Ambedkar National Institute of Technology, Jalandhar. The paper demonstrates the construction and kinematics analysis of the model and its drafting in AutoCad 2002.

The model has also been designed and animated in two softwares - ‘Pro Desktop Express – the desktop version of Pro Engineer’ and Solid Edge. However Pro Desktop was effective of the two and so animation in that application has been presented.

The mechanism is basically a modification of the 3-dimensional slider crank mechanism and is composed of a structure made of wood and the kinematic chain is constituted by a sequence of wooden links whose prime mover is connected to a 3 W A.C. motor. The motion analysis has been initiated with its calculation of Degree of freedom and checking the customized constrains.

The success of the model would be realized when the dynamic force analysis of the model is completed and the stability established in the original model which would follow as our next work.

 

 

 

CHAPTER 1

INTRODUCTION

 

 

1.1  Walking Machines

One need only watch a few slow-motion instant replays on the sports channels to be amazed by the variety and complexity of ways a human can carry, swing, toss, glide, and otherwise propel his body through space. Orientation, balance, and control are maintained at all the times without apparent effort, while the ball is dunked, the bar is jumped, or the base is stolen, and such spectacular performance is not confined to the sports arena-behavior observable at any local playground is equally impressive from a mechanical engineering, sensory motor integration point of view. The final wonder comes when we observe the one year old infant’s wobbly with the knowledge that running and jumping will soon be learned and added to the repertoire.

Walking machines are the advanced alternatives to the wheeled locomotion systems which find applications where wheeled systems cannot operate. Some instances are in hauling loads over soft or irregular ground often with obstacles , agricultural operations , for movements in situations designed for human legs such as climbing stairs , ladders …..

To carry out these operations numerous walking machines have been developed.

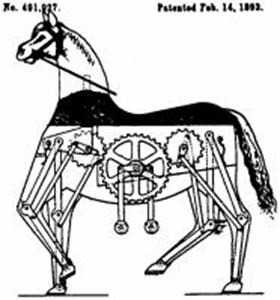
	Fig. Some of the first walking mechanisms

 

 

 

1.1.1        Human – Walking machines analogy

Two-legged walking, running, jumping and skipping are some of the most sophisticated movements that occur in Nature, because the feet are quiet small and the balance at all times has to be dynamic; even standing still requires sophisticated control. If one falls asleep on ones feet he falls over.

The human stabilizes the movement by integrating signals from:

• Vision which includes ground position and estimates of the firmness of the ground and the coefficient of friction.
• Proprioception that is knowledge of the positions of all the interacting muscles, the forces on them and the rate of movement of the joints.
• The vestibular apparatus, the semi-circular canals used for orientation and balance.

A very large number of muscles are used in a coordinated way to swing legs and the muscle in an engine consisting of a power source in series with an elastic connection. The muscle activity is pulsed and there is an energetically optimal walking speed of 3.5 km/hr when the legs swing in a natural oscillation frequency, although they can swing much faster without much extra loss of energy. Various walking machines have been developed to imitate human legs, but none is as efficient as those of humans.

 

1.1.2 Classification of Walking Machines

Walking machines are classified according to the numbers of legs or limbs they constitute. They range from single-legged hopping mechanisms to six to eight-legged mechanisms

They may be

·      One-legged

·      Two-legged

·      Three-legged

·      Four-legged

·      Six-legged

·      Eight-legged

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.1.3 Design aspects

Three important aspects in the design of any walking mechanism

·      Orientation

·      Balance

·      Control

Each of these aspects has to be well controlled for the success of any new design of walking mechanism.

1.2 Stair Climbing Mechanism

Stair Climbing mechanisms are walking machines which have specific target of climbing stairs. Stair Climbing Mechanisms are various and diverse in the mechanisms they are based on.

Dr. Dean Kamen, Founder of FIRST and the President and owner of DEKA Research & Development Corporation, a Manchester, New Hampshire-based company specializing in advanced technologies in medical equipment, is the man who recently revolutionized the field of Stair Climbing mechanisms after he came up with iBOT, a stair-climbing robotic wheelchair

The speciality of iBOT is that the mechanism on which it is based is dynamically stable. Dynamic stability is what every Robotic engineer dreams for in his robot. And that is why the machine has climbed such success.

 

1.3 The Scepter

‘Scepter’ literally means a device which is used by the disabled people. The Scepter’ – name of the Stair Climbing Mechanism designed by us was named so because of the fact that its basic purpose is to aid the disabled. The design, construction, analysis, modeling, animation of the model are discussed in the following chapters.

 

 

 

 

 

 

 

 

 

DESIGN & CONSTRUCTION

 

2.1  Design Introduction

The scepter is a small mechanical system which can walk in a straight path as well as can climb stairs while maintaining static balance all the time. It walks with the help of its two front legs and two wheels. It can climb in stairs up to 2cm. the model is not optimized and moreover the power of the small motor is also another limiting factor. These limiting factors together result in the small height of climb. The small speed is due to the small rpm of the motor used. For legs instead of two can also be used. The model is only an experimental model and shows the basic mechanism. A number of improvements are under development. The final model will be used as a stair climbing wheelchair. The features of the final model will be discussed later.

 

2.2  Description

The different parts of the system are

·      Front-legs

·      Frame

·      Wheels

·      Prime mover (electric motor)

·      Chain

·      Leg aligner link

·      Motion transmitting cam

The function of each part is being discussed as follows.

 

2.3  Front legs

The front legs of the model are made of aluminum to keep the net weight and mass moment of inertia low. The legs are L shaped, so as to counter the longitudinal moment produced by the weight of the system. It actually serves the purpose of two legs. Four front legs can also be used instead of two L-shaped legs. As at any moment two wheels and only one leg is in touch with the ground the legs have to be L-shaped to ensure the stability of the system.

In the future steering of the system will also be done on the front legs themselves. The legs will also be provided with vacuum suction so as to ensure firm hold on the ground.

` While climbing the front legs carry the entire horizontal load. This load is carried by friction in the legs. To decrease this required friction, the rear wheels has also to be powered independently. The power will be provided only when necessary, i.e. when the wheel encounters a stair or a hurdle. This is another development that is under consideration.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.4  Frame

The frame is made of wood. It has to resist the entire load and transmit the power. If the frame wouldn’t be rigid enough, it will deform due to the torque provided by the motor (which actually happened in my first model, which was made of cardboard. So I had to provide wooden beams so as to resist the bending load). When the frame is not rigid enough it itself deforms instead of transmitting the motion. But the frame should be light besides being rigid. So the choice of material is crucial here. The material should be rigid as well as light. As the frame contributes maximum to the weight of the entire system it should be optimized in terms of utilization of material. The structure of the frame should resist the load most economically, i.e. only those parts should be most rigid which are under more loads. The stress analysis can yield the desired value for the rigidity of the section under consideration, which is to be done in future.

 

2.5  Wheels

The wheels are also made of wood. They too share the load of the system. The wheels should have been rimmed instead of discs. The moment of inertia of the wheels should be kept low, so as to keep the required torque low. But due to the non-availability of such small sized rimmed wheels disc shaped wheels are used. It is also the ease of manufacture and mounting of disc shaped wheels that they have been used as wheels. This resulted in the lowering of the maximum efficiency of the system, i.e. the maximum height that could have been climbed is reduced.

While climbing a stair the vertical load is balanced by the friction on the wheels. So the coefficient of friction between the edge of the stair and the wheels has to be sufficient enough so as to balance the vertical load. But there is a limit to the value of the coefficient of friction. So the load that can be carried by them has a limit. The problem can be solved by decreasing the load that is to be carried by the wheels. This can be done by shifting the center of gravity towards the front. That can be done by moving the seat of the wheelchair towards the front. That is the development to be done in the future.

 

2.6  Prime mover

This is a 3 watt and 240 volts electric motor. The rpm of the motor is between 5 and 6. This lightweight and powerful motor is the only source of power. The power is transmitted through a chain. A bush is mounted on the motor which is the link between the motor and the chain. The motor is actually used in the automatic swing attachment in desert coolers. The chain is used in the engine case of Hero Honda motorcycle.

 

2.7  Leg-aligner link

This link is used to align the legs, i.e. this ling is used in order to keep the degrees of freedom of the system one. The leg aligner is mounted on the structure.

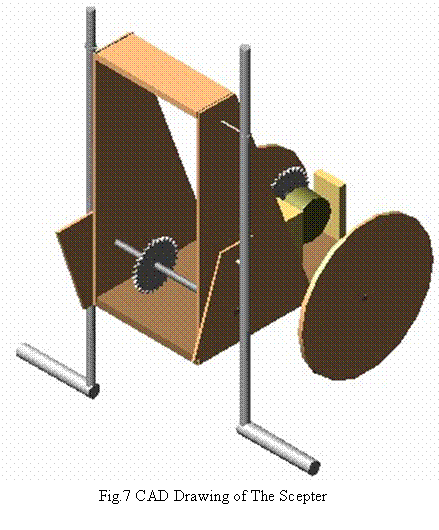
2.8 Motion transmitter cam

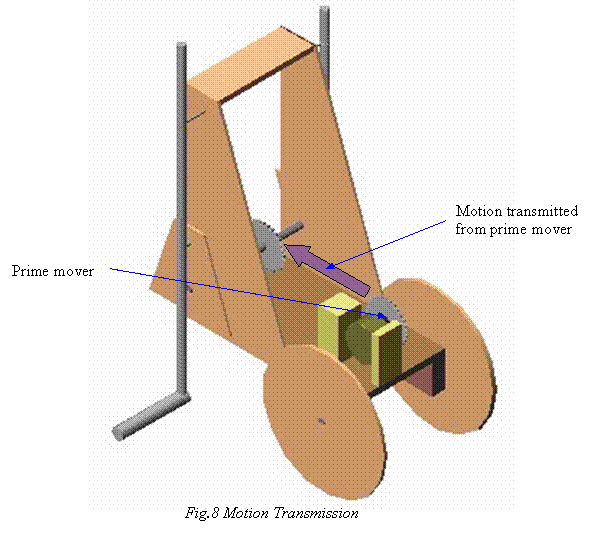This is the most important part of the system. This link changes the circular motion provided by the motor to leg like motion.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

CHAPTER 3

KINEMATIC ANALYSIS

 

 

3.1 Two-Dimensional Equivalent Mechanisms

For the kinematic analysis to begin the best 2-D equivalent or planar form of the mechanism has to be identified.

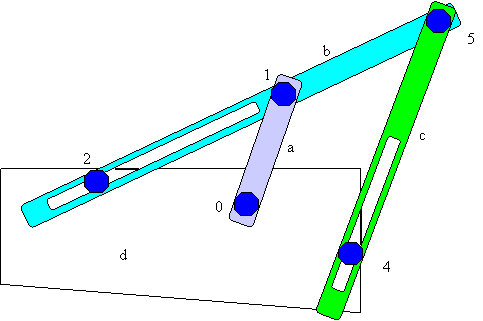
A static 2D Equivalent is shown in fig.10

One of the forms can be fig.9. This would be a dynamic mechanism, i .e, none of the links is made fixed and so the entire system would be in motion. So this is the representation of the actual motion exhibited by the scepter. But analysis of a dynamic mechanism would be much more complicated than that of static one.

 

 

 

 

 

 

 

 

Fig.9 is a two-dimensional representation of the actual mechanism. This mechanism shows the motion of one leg and one wheel. The link a represents the cam (motion transmitter), which initiates the motion. The link a i.e., the cam is given the motion. So it is constrained to move in a particular direction.

The link b is the leg. The point 2 is the leg aligner. It is the part of the structure and this guides the leg while in motion. The kinematic pair between the leg, i.e. a slotted lever and this leg aligner is a higher pair.

The point 4 is the contact point between the wheel and the ground. This is also represented by a slotted leaver link, again a higher pair. As there is no slip between the wheel and the ground, this can be taken as a link while modeling the system in two dimensions.

The point 3 is the contact between the legs and the ground. Again there is no slip between the legs and the ground and hence it was possible to model that as a lower pair.

The link d is the structure and link c is the ground. Thus in total there are 4 links. There should be 5 kinematic pair, out of which 3 are lower and 2 are higher. The details of these kinematic pair are given below.

Between link d and a (frame and cam): lower pair

Between link a and b (cam and leg): lower pair

Between link b and c (leg and ground): lower pair

Between link b and d (leg and leg aligner): higher pair

Between link c and d (ground and wheel): higher pair

The degree of freedom of the system is = 3(4-1)-2*3-2 = 1

As the degree of freedom is found to be 1 the motion is clearly constrained.

The following sections demonstrate the derivation of the velocity and the accelerations expressions for the mechanism.

3.2 Velocity Equations

 

 

 

 

 

 

 

 

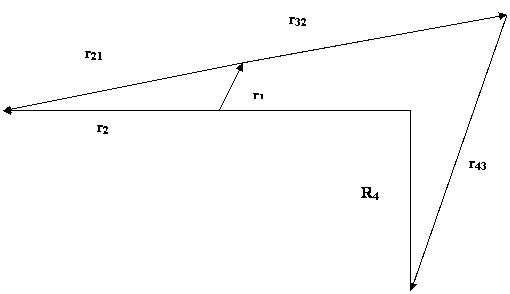
Fig.11 Displacement Diagram

 

 

 

 

 

 

 

 

 

From the geometry of the figure;

r_{2 =} r1 + r₂₁

⇒r₂e^iɵ2 = r₁e^iɵ₁ + r₂₁e^iɵ₂₁ … … … … … … … … … (1)

So differentiating the above geometric expression yields

0 = iɵ̇₁r₁e^iɵ₁ + iɵ̇₁r₂₁e^iɵ_{2 1} + r ̇₂₁e^iɵ_{2 1} … … … … … … … (2)

Now, this equation can be rewritten in trigonometric form as:

0 = r₁ɵ̇₁(icosɵ₁- sinɵ₁) + r₂₁ɵ_̇̇₂₁(icosɵ₂₁ - sinɵ₂₁) + r ̇₂₁(cosɵ₂₁ + isinɵ₂₁) … … … (3)

By equating real and imaginary parts,

0 = -r₁ɵ̇₁sinɵ₁ + r ̇₂₁cosɵ₂₁ – r₂₁ɵ̇₂₁sinɵ₂₁

0 = r1ɵ̇₁cosɵ₁ + r₂₁ ɵ̇_̇21cosɵ₂₁ – r ̇₂₁sinɵ₂₁

The unknowns of these equations are r ̇₂₁ and ɵ̇_̇21. These can be deduced by solving the two equations.

Again from the geometry of the figure:

R₄ = r₄₃ + r₃₂ + r₂

⇒ r₄e^iɵ₄ = r₄₃e^iɵ_{4 3} + r₃₂e^iɵ _{3 2} + r₂e^iɵ₂

Differentiating the above geometric expression yields,

0 = r ̇₄₃e^iɵ_{4 3} + i r₄₃ɵ̇₄₃e^iɵ₄₃ + r ̇₃₂e^iɵ_{3 2} + iɵ̇₃₂r₃₂e^iɵ_{3 2}

This equation can be rewritten in trigonometric form as:

0 = r ̇₄₃ [cosɵ₄₃ + isinɵ₄₃] + r₄₃ɵ̇₄₃ [icosɵ₄₃- sinɵ₄₃] + r₃₂ɵ̇₃₂ [icosɵ₃₂ - sinɵ₃₂]

+ r ̇₃₂[cosɵ₃₂ + isinɵ₃₂]

By equating real and imaginary parts,

0 = r ̇₄₃cosɵ₄₃ - r₄₃ɵ̇₄₃sinɵ₄₃ - r₃₂ɵ̇₃₂sinɵ₄₃ + r ̇₃₂cosɵ₃₂

0 = r ̇₄₃sinɵ₄₃ + r₄₃ɵ̇₄₃cosɵ₄₃ + r₃₂ɵ̇₃₂cosɵ₄₃ + r ̇₃₂sinɵ₃₂

The unknowns of the equation are r ̇₄₃ and ɵ̇₄₃. As ɵ̇₃₂ = -ɵ_̇̇₂₁ and r ̇₃₂ = - r ̇₂₁, the unknowns can be deduced by solving the two equations.

 

3.3 Acceleration Equations

The accelerations can be obtained by differentiating the velocity expressions. The results are:

0 = ir₁ɵ̈₁e^iɵ₁ – (ɵ̇₁)²r₁e^iɵ₁ + ir₂₁ɵ̈₂₁e^iɵ_{2 1} + r ̈₂₁e^iɵ_{2 1} + (ɵ̇₁)² r₂₁e^iɵ_{2 1} + iɵ̇_̇21 r ̇₂₁e^iɵ_{2 1}

(∵ɵ̈₁ = 0, for simplicity)

0 = – (ɵ̇₁)²r₁e^iɵ₁ + ir₂₁ɵ̈₂₁e^iɵ_{2 1} + r ̈₂₁e^iɵ_{2 1} + (ɵ̇₁)² r₂₁e^iɵ_{2 1} + iɵ̇_̇21 r ̇₂₁e^iɵ_{2 1}

This equation can be rewritten in trigonometric form as:

0 = r ̈₂₁ [cosɵ₂₁ + isinɵ₂₁] – r₁ (ɵ̇₁)²[cosɵ₁+ isinɵ₁] + r₂₁ɵ̈₂₁ [icosɵ₂₁ - sinɵ₂₁] - (ɵ̇₁)² r₂₁ [cosɵ₂₁ + isinɵ₂₁] + ɵ̇_̇21 r ̇₂₁ [icosɵ₂₁ - sinɵ₂₁]

By equating real and imaginary parts,

0 = r ̈₂₁cosɵ₂₁ – r₁ (ɵ̇₁)²cosɵ₁- r₂₁ɵ̈₂₁sinɵ₂₁-(ɵ̇₁)²r₂₁cosɵ₂₁ - ɵ̇_̇21 r ̇₂₁sinɵ₂₁

0 = r ̈₂₁sinɵ₂₁ – r₁ (ɵ̇₁)²sinɵ₁ + r₂₁ɵ̈₂₁cosɵ₂₁ + (ɵ̇₁)²r₂₁sinɵ₂₁ + ɵ̇_̇21 r ̇₂₁cosɵ₂₁

The unknowns of the equation are r ̈₂₁ and ɵ̈₂₁ . Solving the 2 equations we can find the unknowns.

Differentiating the second velocity expression, we have:

0 = r ̈₄₃e^iɵ₄₃ + ir₄₃ɵ̈₄₃e^iɵ₄₃ – (ɵ₄₃̇) ^2r43eiɵ43 + iɵ̇_̇43r ̇₄₃e^iɵ_{32 +} ir₃₂ɵ̈₃₂e^iɵ_{3 2} + r ̈₃₂e^iɵ_{2 1} - (ɵ̇₃₂)² r₃₂e^iɵ_{3 2} + iɵ̇_̇32r ̇₃₂e^iɵ_{3 2}

Writing in the trigonometric form,

0 = r ̈₄₃[cosɵ₄₃ + isinɵ₄₃] + r₄₃ɵ̈₄₃[icosɵ₄₃- sinɵ₄₃] – (ɵ₄₃̇)²r₄₃[cosɵ₄₃ + isinɵ₄₃] + ɵ̇_̇43r ̇₄₃ [icosɵ₄₃- sinɵ₄₃] + r₃₂ɵ̈₃₂[icosɵ₃₂ - sinɵ₃₂]+ r ̈₃₂[cosɵ₃₂ + isinɵ₃₂] -(ɵ̇₃₂)² r₃₂[cosɵ₃₂ + isinɵ₃₂]+ ɵ̇_̇32r ̇₃₂[icosɵ₃₂ - sinɵ₃₂]

By equating real and imaginary parts,

0 = r ̈₄₃cosɵ₄₃ - r₄₃ɵ̈₄₃ sinɵ₄₃ – (ɵ₄₃̇)² r₄₃cosɵ₄₃ - ɵ̇_̇43r ̇₄₃ sinɵ₄₃- r₃₂ɵ̈₃₂sinɵ₃₂+ r ̈₃₂cosɵ₃₂ - (ɵ̇₃₂)²r₃₂cosɵ₃₂ - ɵ̇_̇32r ̇₃₂sinɵ₃₂

0 = r ̈₄₃sinɵ₄₃ + r₄₃ɵ̈₄₃ cosɵ₄₃ – (ɵ₄₃̇)² r₄₃sinɵ₄₃ + ɵ̇_̇43r ̇₄₃ cosɵ₄₃ + r₃₂ɵ̈₃₂cosɵ₃₂+ r ̈₃₂sinɵ₃₂ - (ɵ̇₃₂)²r₃₂sinɵ₃₂ + ɵ̇_̇32r ̇₃₂cosɵ₃₂

The unknowns of the equation are ɵ̈₄₃ and r ̈_43. Solving the 2 equations we can find their values.

(∵ ɵ̈_{32 =} - ɵ̈_21, and r ̈₃₂ = - r ̈₂₁)

Thus we can find the velocities and accelerations at any point in the mechanism.

 

 

 

CHAPTER 4

MODELLING & ANIMATION

 

 

 

4.1 Methodology

The methodology for modeling and animation of the mechanism:

• Model the parts of the model
• Assemble them
• Define the grounded link
• Define constrains between the mating parts
• Define motion to the parts
• Create frames for different positions of the model sequentially
• Save as an *.avi or *.mpg file

 

4.2 Softwares used

The animation has been done in two softwares.

• Pro Desktop Express
• Solid Edge

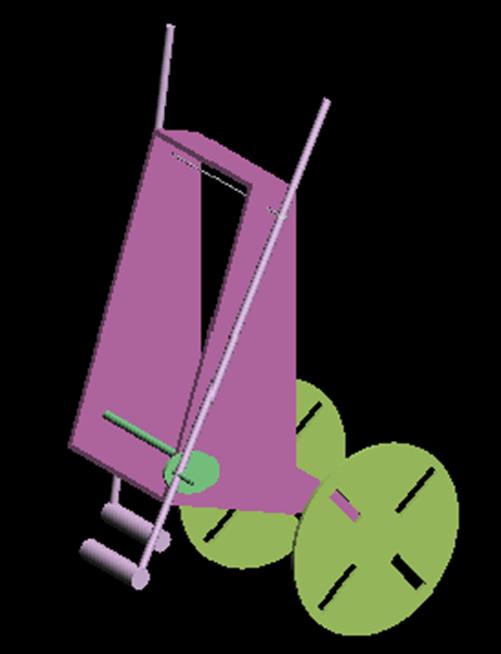
But only the work done in Pro Desktop Express is presented. (fig.12)

 

 

	Fig.12 Model animated in Pro Desktop Express

 

 

 

CHAPTER 5

CONCLUSIONS

 

 

5.1 Result

After numerous demonstrations and trials, the maximum height of the stairs, ‘The Scepter’ can climb is standardized at 4cms

 

5.1 Limitations

·        Power of the motor insufficient to lift the structure.

·        Moment of Inertia of the wheel is high since it’s an wooden disk. It should have been a circular ring.

·        Friction at the contacts of the legs with the surface is not optimum.

·        Friction at the joints is also quite high since it’s a wooden system.

 

5.2 Future Scope

·        Steering mechanism: a slider crank mechanism at the feet to offset the contact with the surface.

·        Self-defined ellipse system:

v     An hydraulic or an pneumatic system to be used to vary the major and minor axes

v     Sensors can be used to decide determine the dimensions of the stairs to be climbed.

·        Vacuum contact system at the legs

·        Sensors to stimulate all the above mechanisms automatically

·        Powering the rear wheels

·        Horizontally maintained seat (here base plate)

 

 

 

 

REFERENCES

 

 

 

Web sites

·        http://www.neuroprosthesis.org/dkamen.htm

·        http://www.delphion.com

·        http://ls11-www.cs.uni-dortmund.de/people/ziegler/RoboterLaufen2Legs.html

·        http://web.mit.edu

·        http://www-personal.engin.umich.edu/passive_walking.html